In FHIR, there’s a neat feature called implicit ValueSets. These don’t need to be defined or published anywhere. They exist because the server knows how to interpret the request. You ask for an expansion, and the server builds the ValueSet on the fly. No authoring. No versioning. No fuss.… read more...
An off the shelf terminology solution can save developers a lot of time. However, depending on the feature set offered, you can lose a lot of the capabilities provided by SNOMED CT. Especially so with a FHIR server, whose standardised API supports text searching and subsumption, but little else in … read more...
Today I saw the following enquiry:
“Unfortunately, the software on our automated dispensing cabinets can only accept values up to 15 characters long…”
This is unfortunate, because of the almost 6000 MPUUs in AMT, only 10 are 15 characters or less. And it isn’t the first time the length … read more...
Recently I was shown this curious subhierarchy in SNOMED CT
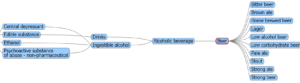Beer IS A Ethanol?
My first response was that these things are mixtures. And as such should have a contains or has ingredient type of relationship. Beer contains ethanol.
Which then raises the idea that these things are … read more...
There’s a few ways to work with a FHIR terminology server in C#. My goal in these examples is to find a code (and return the preferred term) with the term “inr” from the SNOMED CT-AU refset 1072351000168102. For all these, I’ll be using the same endpoint:
Since it’s … read more...
The IHTSDO has a preference to define concepts by Closest proximal primitive (CPP) parent(s). I’m yet to be convinced of the benefit of this approach, and prefer stating any obvious parent (regardless of their definition status) along with a set of defining attributes that are independent of whatever parents … read more...
Some time back I learnt of a feature of description logic – general concept inclusions (GCI). It took me a while to get my head around the idea, but I found this post the most effective, at least for me, in understanding what they were about. The first potential application … read more...
One of the things that frequently talked about in AMT (both V2 and V3) has been the “7 boxes”. From my experience when the AMT model is being discussed, it’s always presented as a single monolithic thing, specifically as per this image below (original available here). However, I feel … read more...
I’ve noticed the first time some people are exposed to the outcome of a SNOMED CT classification they regard it some form of black magic because they don’t like what it does and/or don’t understand why it’s done what it has done.
If they don’t like what it has done, … read more...
Yesterday I was explaining to a colleague that reference sets can be used to do all sorts of interesting things other than just describe basic subsets of content, when I realised an option I’d not considered before…
The SNOMED CT RF2 specification details a core structure of 6 fields (the … read more...